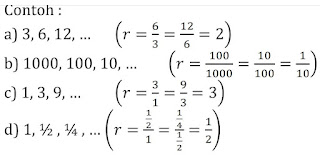Postingan

Barisan Aritmatika

-
Gambar
Barisan aritmatika adalah barisan bilangan yang selisih antara dua suku yang berurutan sama atau tetap. Barisan dari aritmatika dapat di artikan sebagai susunan bilangan yang real dan membentuk pola tertentu. Kemudian arti dari deret aritmatika sendiri iyalah sebuah penjumlahan dari barisan aritmatika. Dan ciri – ciri umum nya dari barisan aritmatika yaitu mempunyai beda yang sama dari satu bilangan ke bilangan yang berikut nya. Contoh dari barisan aritmatika ialah seperti di bawah ini : a)       3, 8, 13, 18, …. (selisih/beda = 8 – 3 = 13 – 8 = 18 – 13 = 5 )  b)       10, 7, 4, 1, …. ..(selisih/beda = 7 – 10 = 4 – 7 = 1 – 4 = – 3)  c)       2, 4, 6, 8, …. …(selisih/beda = 4 – 2 = 6 – 4 = 8 – 6 = 2)  d)       25, 15, 5, –5, …(selisih/beda = 15 – 25 = 5 – 15 = –5 – 5 = –10) Jika suku pertama = a dan beda = b, maka secara umum barisan Aritmetika tersebut adalah: U 1                     U 2                    U 3                   U 4                     U n a,            
Posting Komentar
Baca selengkapnya

Deret Aritmatika

-
Gambar
Deret Aritmetika adalah jumlah dari seluruh suku-suku pada barisan aritmetika. Jika barisan aritmetikanya adalah U 1 , U 2 , U 3 , …., U n maka deret aritmetikanya U 1 + U 2 + U 3 + …. +U n dan dilambangkan dengan S n           S n = U 1 + U 2 + U 3 + ……………………………………    +U n           S n = a + (a + b) + (a + 2b) + … + (U n – 2b) + (U n – b) + U n           S n = U n + (U n – b) + (U n – 2b) + …. + (a + 2b) + (a + b) + a            2 S n = (a + U n ) + (a + U n ) + (a + U n ) + …. + (a + U n ) + (a + U n ) + (a + U n )           2 S n = n (a + Un) Karena Un = a + (n – 1)b maka jika disubstitusikan ke rumus menjadi Keterangan : S n = Jumlah n suku pertama deret aritmetika U n = Suku ke-n deret aritmetika a = suku pertama b = beda n = banyaknya suku Untuk menentukan suku ke-n selain menggunakan rumus U n = a + (n – 1)b dapat juga digunakan rumus yang lain yaitu : Tentukan jumlah 20 suku pertama deret 3 + 7 + 11 + … Pembahasan : Mencari beda dengan meng
Posting Komentar
Baca selengkapnya

Suku Tengah

-
Gambar
Suku Tengah Barisan Aritmatika Suku tengah suatu barisan aritmatika hanya terdapat pada barisan aritmatika yang memiliki suku ganjil. Perhatikan tabel di bawah ini : Suatu barisan aritmatika dengan banyak suku adalah ganjil (2t - 1), dengan t bilangan asli lebih dari dua. Suku tengah dari barisan aritmatika itu adalah suku ke-t atau U t dan rumus suku tengah  U t ditentukan oleh hubungan : U t = ½ (a + U n )       atau       U t = ½ (U 1 + U 2t-1 ) Barisan aritmatika yang jumlahnya ganjil dan minimal terdiri dari 3 suku memiliki suku tengah  dimana : U t = a + (t-1).b Contoh Soal : 1.       Diketahui barisan aritmatika 15,18,21,...,231. Tentukan suku tengahnya dan merupakan suku keberapa? Jawab: Barisan aritmatika : 15,18,21,...,231 Diperoleh: a = 13, b = 3, dan U n = 231 U t = ½ (a + U n )      = ½ (15 + 231 )      = 123 Jadi, suku tengahnya adalah 123   U t = a + (t-1).b 123 = 15 + (t-1).3 123 = 15 + 3t – 3 123 = 3t + 12 111 = 3t t
Posting Komentar
Baca selengkapnya

Sisipan pada Baris Aritmatika

-
Jika hendak membuat sebuah baris aritmatika dengan telah diketahui nilai suku pertama (a) dan suku terakhirnya (p), dapat disisipkan sejumlah bilangan diantara keduan bilangan tersebut. Sejumlah bilangan (q buah) tersebut menjadi suku-suku baris aritmatika dan memiliki selisih antar suku beredekatan (b). Baris aritmatika tersebut memiliki jumah suku q + 2 dan diurut berupa: a, (a + b), (a + 2b), (a + 3b), …, (a + q.b), (a + (q+1)b) Diketahui bahwa suku terakhir: (a + (q+1)b) = p Maka, nilai b dapat ditentukan sebagai: b = (p - a) / (q + 1)   Misalkan a= 1 dan p = 9, jika disisipkan 3 bilangan diantara a dan p, maka baris belangan aritmatikanya adalah : Nilai q = 3 Jumlah suku = q + 2 = 3 + 2 = 5 b = (9 - 1) / (3 + 1) = 8/4 = 2 Baris aritmatika : 1 , 3 , 5 , 7 , 9
Posting Komentar
Baca selengkapnya

Contoh Soal

-
  Contoh Soal Barisan dan Deret Aritmatika 1. Suku ke-40 dari barisan 7, 5, 3, 1, ... adalah ... Pembahasan: Diketahui: a = 7 b = -2 Ditanya: U 40 = ... ? Jawab: U n = a + (n-1).b U 40 = 7 + (40-1).(-2) U 40 = 7 + (39).(-2) U 40 = 7 + (-78) U 40 = 7 – 78 U 40 = -71 Jadi, suku ke-40 barisan aritmatika tersebut adalah -71.   2.    2.  Rumus suku ke-n dari barisan 5, -2, -9, -16, ... adalah ... Pembahasan: Diketahui: a = 5 b =-7 Ditanya: rumus suku ke-n barisan aritmatika tersebut...? Jawab: U n = a + (n-1).b U n = 5 + (n-1)(-7) U n = 5 -7n + 7 U n = 12-7n Jadi, rumus suku ke-n barisan aritmatika tersebut adalah 12 - 7n   3.  3.  Dalam suatu gedung pertunjukkan disusun kursi dengan baris paling depan terdiri dari 12 kursi, baris kedua berisi 14 kursi, baris ketiga berisi 16 kursi, dan seterusnya. Banyaknya kursi pada baris ke-20 adalah ... Pembahasan: Diketahui: a = 12 b = 2 Ditanyakan U 20 Jawab: U n = a + (n-1)b
Posting Komentar
Baca selengkapnya

Barisan Geometri

-
Gambar
  BARISAN GEOMETRI Barisan geometri adalah suatu barisan bilangan yang hasil bagi dua suku yang berurutan selalu tetap (sama). Hasil bagi dua suku yang berurutan disebut rasio (r) Contoh: Jika suku pertama dari barisan geometri U1 = a dan rasio = r, maka barisan geometri tersebut adalah Diketahui barisan geometri 3, 6, 12, ... tentukan suku ke 10! Pembahasan: Barisan geometri: 3, 6, 12, … a = 3, 𝑟 = 6/3 = 2 , dan n = 10 Maka   U n = a.r n-1 U 10 = 3 . (2) 10 – 1 U 10 = 3 . (2) 9 U 10 = 3 . 512 U 10 = 1536 Jadi, nilai 𝑈 10 = 1536 Suatu barisan geometri diketahui U 3 = 144 dan U 7 = 9. Tentukan U 6 Pembahasan: Untuk bisa menentukan  U 6  maka harus tahu nilai a dan r 1. Nilai r bisa didapatkan dari : 2. Nilai a bisa didapatkan dari :
Posting Komentar
Baca selengkapnya